원본: A tutorial quantum interpreter in 150 lines of Lisp (Snapshot) by Robert Smith
[1일 약 1챕터 단위로 번역중]
(위 이미지는 역자가 Emacs와 SLY로 실행중인 본 문서의 함수들이다. SLY 인터페이스에서 이미 스쳐 지나간 연말의 향기가 나는 것 같다)
범용적인 게이트 기반 양자 컴퓨터를 고전 컴퓨터로 시뮬레이션하는 것에는 많은 사용처와 이점이 존재한다. 가장 큰 이점은 반응계 상태의 진폭을 직접적으로 조사할 수 있다는 점이다. 그러나, 그 수학적 측면이 잘 이해된 것에 비해, 범용 시뮬레이터를 구현하는 과정은 대체로 민간전승에 가까운 지식을 동반한다. 본 튜토리얼에서는, 문헌에서 찾을 수 있는 대부분의 양자 회로를 실행할 수 있는, 우리가 \(\mathscr{L}\)이라 부르는 범용 양자 프로그래밍 언어를 위한 인터프리터의 제작 과정을 설명한다. 이는 경제 효율적으로 제시되며, 그 구현체는 150줄 미만의 독립적 Common Lisp 코드가 될 것이다. 언어 \(\mathscr{L}\)은 확장하기 쉬우며, 이는 그 인터프리터로 하여금 노이즈와 같은 다양한 성질을 테스트하기 걸맞게 만든다.
1. 시작하며
이상적인 양자 컴퓨터의 움직임을 시뮬레이션하는 것은 알고리즘 연구 및 양자 프로그램 디버깅 등, 많은 적용 가능성을 가지고 있다. 다양한 양자 컴퓨터 시뮬레이터들이 현존하며, 자유/무료인 것도 상업적인 것도 존재한다. 하지만 양자 컴퓨터의 개념이 고레벨 층위에서 쉽게 이해될 수 있는 데 반해, 구현을 논하게 되면 디테일한 곳에서 문제가 발생하는 법이다.
손에 넣을 수 있는 각종 양자 컴퓨터 시뮬레이터들에는 종종 많은 한계들이 존재한다. 가장 흔한 한계점은 연산자 (역주: 현상적 측면에서는 게이트와 동일시해도 무방할 것이다) 가 작용할 수 있는 큐비트의 개수일 것이다. 일반적으로, 1 Qubit 게이트와 controlled one-qubit 게이트 1 들이 허용되는데, 그뿐이다. 이 둘만 해도 범용 양자 연산에는 충분하지만, 양자 알고리즘의 연구를 위해서는 좀 더 욕심을 내 볼 법하다.
이 글에서는, 관측을 포함하여, 임의의 유니터리 연산자들로 하여금 임의의 개수의, 임의로 배치된 큐비트들에 대한 연산을 수행 가능한 완전 범용 양자 프로그래밍 언어의 인터프리터를 제시할 것이다. 구현된 결과물은 150줄 미만의 LISP 코드가 될 것이며, 그 개념의 단순성은 타 언어로의 실장 또한 손쉽게 만들 것이다. 튜토리얼의 코드는 GitHub에서 찾을 수 있다.
본 튜토리얼은 선형 대수와 컴퓨터 프로그래밍에 어느 정도 친숙한 양자 컴퓨팅의 초심자를 위해 쓰여졌다. 그러한 외부 과목들을 제외하고, 이 튜토리얼은 비교적 독립적으로 기능한다. 본 튜토리얼은 또한 양자 컴퓨터의 구체적 세부 사항들에 관심이 있는 실전 경험자/실무자들을 위해서도 쓰여졌다. 문서의 상당 부분이 큐비트와 유니터리 연산자를 설명하는 데 할애되었으므로, 실무자 여러분은 빠르게 훑어보면 될 것이다.
Common Lisp에 대하여
우리는 Common Lisp를 선택했는데, 탐구적이면서도 고성능 컴퓨팅에 걸맞는 최적의 플랫폼이었기 때문이다. 현존하는 가장 빠르고 유연한 양자 시뮬레이터 중 하나인 Quantum Virtual Machine은 온전히 Common Lisp로 쓰여졌다.
이 글은 Common Lisp와 함께 실습해 나가기 쉽게 만들어졌다. 코드에는 의존성이 없고, (바라건대) ANSI 표준을 지키는 모든 구현체에서 작동할 것이다.
말이 나온 김에, 이것이 이식성 또한 염두에 두고 쓰였다는 것을 언급해 두어야겠다. Lisp만의 특색이 있는 기능의 사용을 피했으니, 이 코드는 파이썬이나 C등의 타 언어로 이식하는 것도 손쉬울 것이다. 최소한 언어가 복소수와 배열을 지원한다는 전제 하의 이야기다.
양자 컴퓨팅 실무자들에게
이 단락은 본 문서를 우연히 마주하게 된 경험 많은 실무자들을 위해 쓰여졌으며, 뛰어넘어도 된다.
2. 언어 \(\mathscr{L}\)
이제부터 작은 양자 프로그래밍 언어 \(\mathscr{L}\)을 위한 인터프리터를 작성할 것이다. 이 언어는 양자 컴퓨터의 기초적인 연산 두 가지, 즉 게이트와 측정을 지원한다.
게이트 는 양자 상태를 수정하는 연산이다. (양자 상태가 무엇인지에 관해서는 잠시 뒤에 다룰 것이다.) 양자 상태는 그것을 구축하기 위한 자원보다 「크기」때문에, 게이트는 양자 컴퓨터의 강력한 연산을 대표한다.
측정 은 곧 양자 상태에 대한 관측과 그에 따른 상태의 붕괴 (각 큐비트로부터 고전적 정보로써의 0 또는 1을 반환하는) 를 의미한다. 측정은 우리가 시뮬레이팅할 양자 컴퓨터로부터 우리에게로 정보가 보여질 수 있는 유일한 과정이며, 대부분의 양자 컴퓨터 프로그래밍 모델에서도 이는 마찬가지이다.
언어 \(\mathscr{L}\)은, 비자명하면서 가장 간단한 양자 프로그래밍 언어로 불릴 수도 있다. \(\mathscr{L}\)로 쓰인 프로그램은 게이트와 측정의 나열로 구성되어 있다. 문법은 다음과 같다:
| 비말단 기호Non-Terminal | 정의Definition |
|---|---|
| program | \(:=\) ( instruction* ) |
| instruction | \(:=\) ( GATE matrix qubit+ ) |
\(\vert\) ( MEASURE ) |
|
| matrix | \(:=\) a complex matrix #2A ( … ) |
| qubit | \(:=\) a non-negative integer |
공백 기호와 줄바꿈은 생략되었다. 하지만 언어의 토큰 구분에서는 예외다.
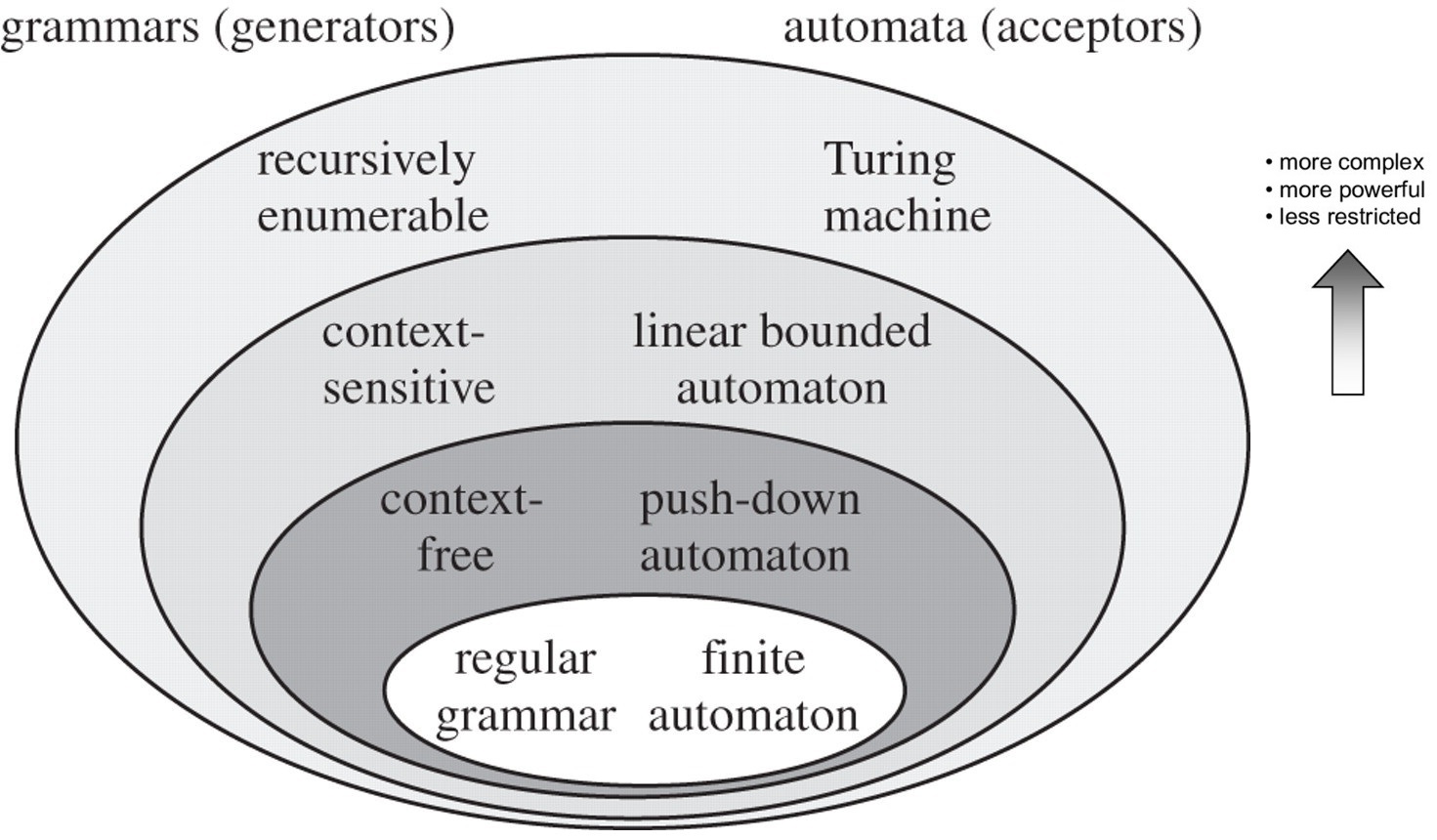
역주: 위 테이블의 형식에 익숙하지 않다면 촘스키 위계 (Snapshot)에 대해 읽어 보는 것을 추천한다. 노엄 촘스키는 언어가 4가지 문법 유형을 가지고 있다고 정의했다. (이미지: (Fitch, 2014))
그리고 여기서 사용되는 비말단 기호Non-Terminal 는 촘스키 위계에서의 Context-Free 언어, 즉 그 문맥에 따라 의미가 변하지 않는 문법을 정의하기 위해 사용되는 배커스 나우르 형식 (BNF) 에서 사용되는 3가지 개념들 (Terminal, Non-Terminal, Expression) 중 하나이다. 언어 파서의 입장에서 말하자면, 비말단 기호는 아직 추가 파싱의 여지가 남아 있는 개념이라 할 수도 있겠다. 말단 기호에 도달하면 epoché가 선언되며 파서는 판단을 중지한다. 이것을 비트겐슈타인이 말하는 원자 명제 와 동일시할 수도 있을 것이다. 이 경우 비말단 기호는 러셀의 유형 계층에서 제시되는, 원자명제들로 구성된 n차 유형이라 생각될 수 있다. (Wittgenstein, 2023)
여기서 Common Lisp의 2차원 배열 문법이 차용되었다. Common Lisp의 경우, 행렬 \(\big(\begin{smallmatrix}
1 & 2\\
3 & 4
\end{smallmatrix}\big)\) 는 #2A((1 2) (3 4)) 로 표기된다. 복소수의 표기 또한, \(1 - 2i\) 는 #C(1 - 2) 로 표기한다.
하나의 예제 프로그램으로써, 각각 2 와 5 라고 명명된 두 개의 큐비트를 벨 상태Bell State 로 구축하고 측정하는 것이 가능할 것이다:
( (GATE #2A((0.70710677 0.70710677) (0.70710677 -0.70710677)) 2)
(GATE #2A((1 0 0 0) (0 1 0 0) (0 0 0 1) (0 0 1 0)) 2 5)
(MEASURE)
)
우리는 추상 기계abstract machine 의 방법에 준거하여 \(\mathscr{L}\)의 의미론을 연산자 기반으로 구축할 것이다. \(\mathscr{L}\)을 위한 추상 기계는 \(M_n\)이며, 여기서 \(n\)은 양의 고정 상수이다. 기계 \(M_n\)의 상태는 순서쌍 \((v, b)\) 이며, 여기서 \(v\)는 양자 상태, \(b\)는 \(n\)비트 길이의 측정값 레지스터다.
양자 상태는 다음 집합의 원소이다:
\(\{ \Vert v \Vert = 1 | v \in \mathbb{C}^{2^{n}} \}.\)
다르게 말하면, \(v\)는 \(2^n\)차원 복소 차원의 단위 벡터에 해당한다. 이것에 대해서는 다음 섹션에서 기초부터 찬찬히 이야기해 보기로 한다.
측정값 레지스터는 집합 \(\{0, 1\}^n\)의 원소이다. 그러니까 n비트의 수열이며, 우리는 이것을 음수를 제외한 정수로 생각할 수 있다. 이 정수의 끝에서 \(k\)번째 자리에 있는 비트는 \(k\)라 명명된 큐비트의 마지막 관측 결과를 나타낸다. 이것에 대해서도 추후 더 자세히 설명할 것이다.
Common Lisp에서 이를 구현하기 위해서는, 2가지 종류의 상태를 가진 machine 구조체를 정의하는 것으로 충분하다.
(defstruct machine
quantum-state
measurement-register)
통상적으로, 이 기계는 관측 레지스터의 0번 위치에서, 각 큐비트는 zero-state에서 시작한다. (그렇지만 알고리즘 연구 및 디버깅을 위하여, 이는 다른 어떤 유효한 상태로도 초기화될 수 있다.)
기계 \(M_n\)이 언어 \(\mathscr{L}\)을 해석하는 적확한 방식은 이 튜토리얼에서 설명될 것이다. 하지만 그 전에, 우리는 양자 상태가 정확히 무엇이며, 이를 컴퓨터에서 표현하려면 어떻게 해야 하는지를 반드시 짚고 넘어가야 한다.
3. 양자 상태
큐비트는 어디에 존재하는가?
역자 참고 문헌Translator’s References
Footnotes
이는 사실상 2큐비트다 (역주: Control 큐비트를 포함할 경우를 말하는 것으로 보임)↩︎